Laguerre basis functions (LBFs)
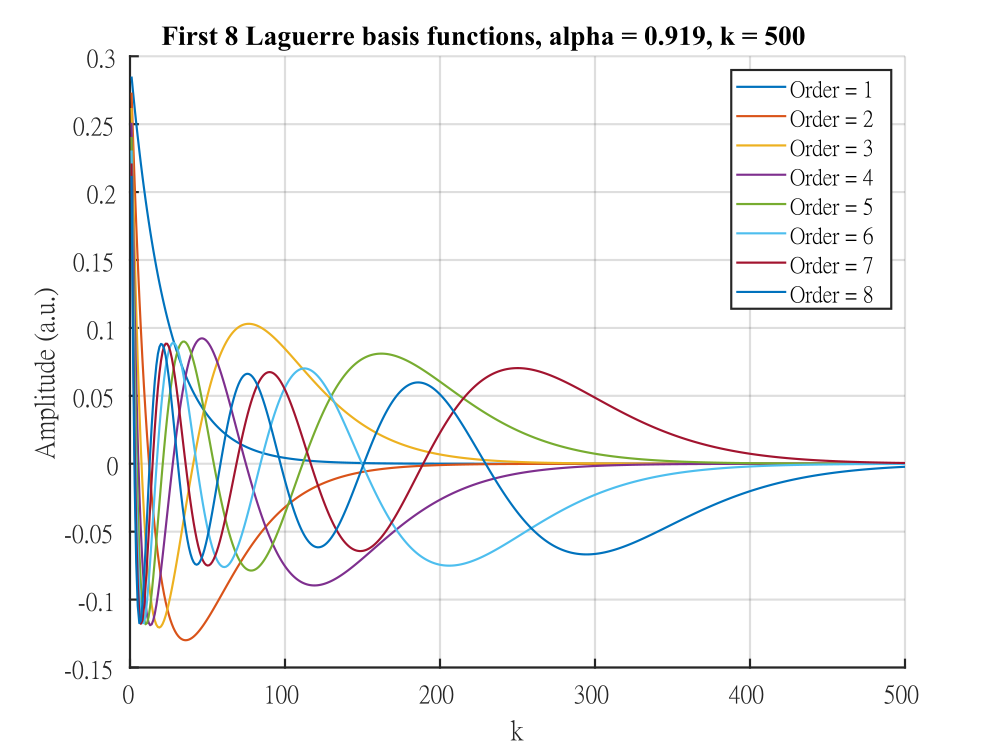
LBFs set is specified by two parameters: scale α and order L. The selection of these two parameters will determine the lifetime range that can be accurately retrieved.
Computational methods for simultaneous, reliable and accurate analysis of fluorescence intensity decay profiles from time-resolved measurements of tissues play an important role in the advancement of FLIm techniques as practical tools in biomedical research and clinical diagnostics. In the context of time-domain fluorescence techniques, the measured fluorescence signal from biological tissues to a light excitation pulse is a convolution of the intrinsic fluorescence decay with the instrument impulse response function (IRF) representing the distorted light pulse due to instrument electronics and other delay components.
Numerous mathematical tools have been devised for the recovery of the intrinsic fluorescence decay. Our lab has developed the Laguerre expansion method in which the intrinsic fluorescence decay is expanded onto an ordered basis set of orthonormal functions, namely Laguerre basis functions (LBFs). This expansion does not make assumptions on the number of fluorophores present in the sample. Instead, the Nonlinear least square estimation is used to find the expansion coefficient that best fits to the observed data after re-convolving with IRF in the least-squares sense. This method is fast and robust compared to the traditional multiexponential decay deconvolution method. Real time recovery of fluorescence lifetime (µs processing time) is achieved for clinical diagnosis.
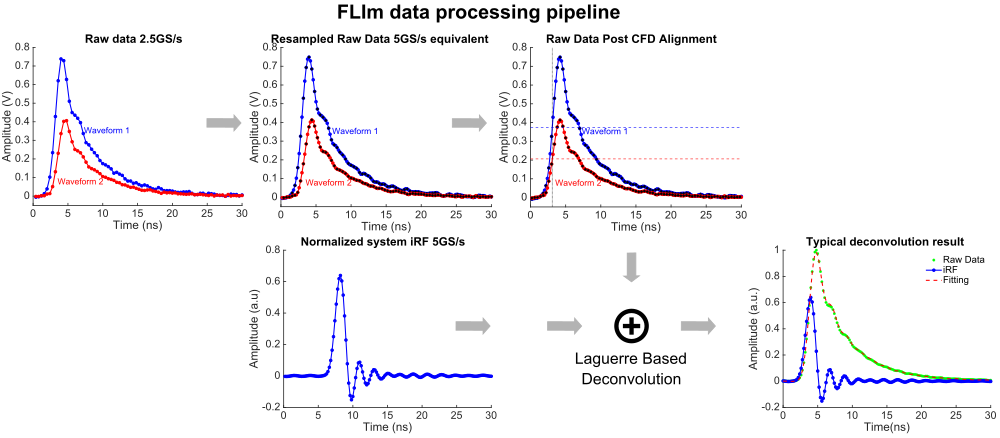
FLIm signal processing pipeline. Fluorescence waveforms from all measurements were temporally aligned using a constant fraction discriminator to compensate for laser jitter. The signal is then deconvolved using Laguerre expansion-based method to extract fluorescence lifetime and intensity. A fluorescence lifetime map can be generated for scanning applications.
Funding
NIH (National Institutes of Health): R01HL67377, R21RR025818